Home Articles posted by Patrick Andrews

Beyond everyday mathematics

“Paradoxically, there are many situations where it is actually easier to solve a general problem than it is to solve a specific one.

I also think that this underscores the importance of being willing to learn outside the classroom.”

See this post for a glimpse into the mind of the young Feynman.

 

Unsolved problems in teaching maths

I found this video inspiring.

Using unsolved problems in mathematics to teach schoolchildren, if done well, is a great way to build confidence. Just telling young people ‘here is a problem which is simply stated, but which the greatest minds can’t solve’ really gets them interested -and using their natural creativity, rather than looking for some boring, half-remembered algorithm.

A map of mathematics

This video makes a good stab at mapping out the entire subject. Something like this would be a useful addition to all maths courses.

I’d really like to understand WHY we have selected some bits for inclusion in public exam curricula and left other bits out. My suspicion is that it’s based on the preferences of various senior academics. As usual, these political types don’t care much about whether this material will actually help young people -either in daily life or in higher study.

This contributes to the feeling that studying maths is about gathering a basketful of disconnected tools. It should be more integrated -and having in mind the big picture would greatly help.

Definition of a reversible process

rev1Note here the reference to ‘one-way work transfer’. Work is not a process in itself, but an exchange of energy (which may form part in a process). It therefore makes little sense to talk about reversible or irreversible work. Nonetheless there are recognisable differences between, say, the work that is done by a stirrer and the work that is done by a piston in quasi-equilibrium.

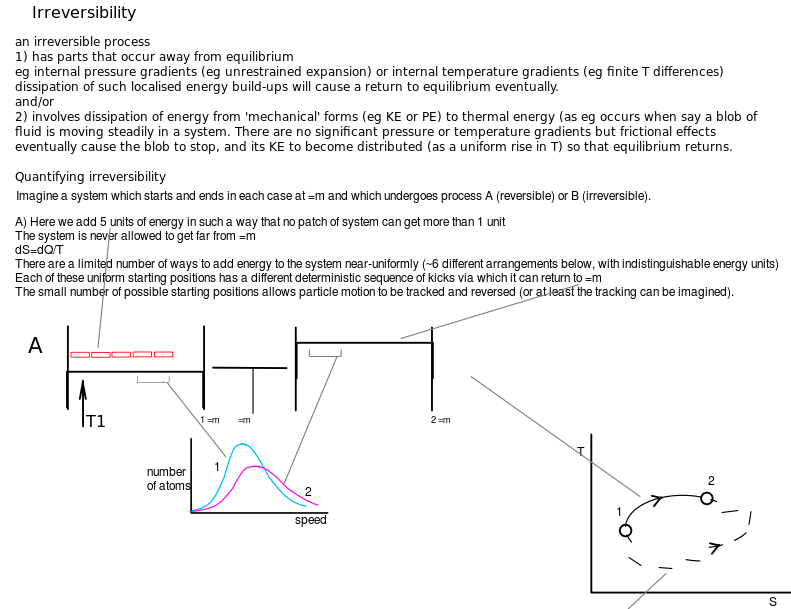
Stirrer work is a transfer of energy which results in dissipation (change of energy from mechanical, bulk or coordinated motion to the thermal (pseudorandom) motion of particles).

Allowing the stirrer freedom to rotate in the opposite direction does not cause energy extraction from the stirred system, however. The stirrer shaft does not spontaneously rotate in the opposite direction and unstir the system contents (hence the term one-way).

Quasi-equilibrium piston work causes zero dissipation. Allowing the piston motion to reverse direction (by reducing the force on the piston to a level infinitesimally less than the force due to internal pressure) does cause the extraction of energy from the compressed system, hence the term two-way work.

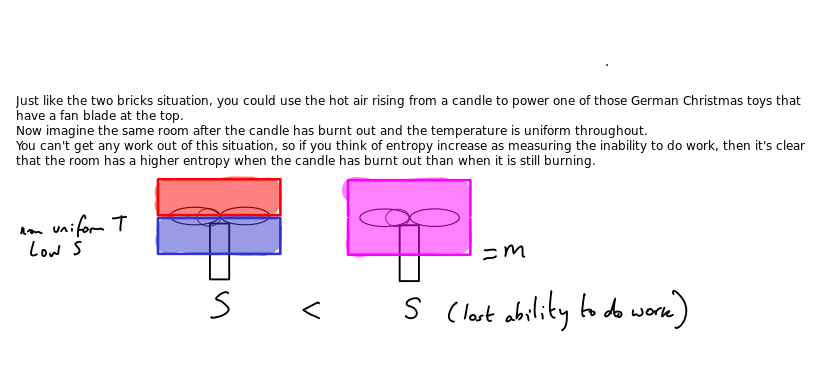
I have already talked about the heat transfer aspect of reversibility. The diagram above is correct but does not explain the situation clearly enough.